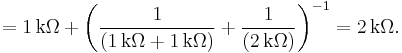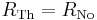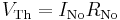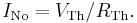Thévenin's theorem
In circuit theory, Thévenin's theorem for linear electrical networks states that any combination of voltage sources, current sources, and resistors with two terminals is electrically equivalent to a single voltage source V and a single series resistor R. For single frequency AC systems the theorem can also be applied to general impedances, not just resistors. The theorem was first discovered by German scientist Hermann von Helmholtz in 1853,[1] but was then rediscovered in 1883 by French telegraph engineer Léon Charles Thévenin (1857–1926).[2][3]
This theorem states that a circuit of voltage sources and resistors can be converted into a Thévenin equivalent, which is a simplification technique used in circuit analysis. The Thévenin equivalent can be used as a good model for a power supply or battery (with the resistor representing the internal impedance and the source representing the electromotive force). The circuit consists of an ideal voltage source in series with an ideal resistor.
Contents |
Calculating the Thévenin equivalent
To calculate the equivalent circuit, the resistance and voltage are needed, so two equations are required. These two equations are usually obtained by using the following steps, but any conditions placed on the terminals of the circuit should also work:
- Calculate the output voltage, VAB, when in open circuit condition (no load resistor—meaning infinite resistance). This is VTh.
- Calculate the output current, IAB, when the output terminals are short circuited (load resistance is 0). RTh equals VTh divided by this IAB.
The equivalent circuit is a voltage source with voltage VTh in series with a resistance RTh.
Step 2 could also be thought of as:
- 2a. Replace voltage sources with short circuits, and current sources with open circuits.
- 2b. Calculate the resistance between terminals A and B. This is RTh.
The Thévenin-equivalent voltage is the voltage at the output terminals of the original circuit. When calculating a Thévenin-equivalent voltage, the voltage divider principle is often useful, by declaring one terminal to be Vout and the other terminal to be at the ground point.
The Thévenin-equivalent resistance is the resistance measured across points A and B "looking back" into the circuit. It is important to first replace all voltage- and current-sources with their internal resistances. For an ideal voltage source, this means replace the voltage source with a short circuit. For an ideal current source, this means replace the current source with an open circuit. Resistance can then be calculated across the terminals using the formulae for series and parallel circuits. This method is valid only for circuits with independent sources. If there are dependent sources in the circuit, another method must be used such as connecting a test source across A and B and calculating the voltage across or current through the test source.
Example
In the example, calculating the equivalent voltage:
(notice that R1 is not taken into consideration, as above calculations are done in an open circuit condition between A and B, therefore no current flows through this part, which means there is no current through R1 and therefore no voltage drop along this part)
Calculating equivalent resistance:
Conversion to a Norton equivalent
A Norton equivalent circuit is related to the Thévenin equivalent by the following:
Practical limitations
- Many, if not most circuits are only linear over a certain range of values, thus the Thévenin equivalent is valid only within this linear range and may not be valid outside the range.
- The Thévenin equivalent has an equivalent I-V characteristic only from the point of view of the load.
- The power dissipation of the Thévenin equivalent is not necessarily identical to the power dissipation of the real system. However, the power dissipated by an external resistor between the two output terminals is the same regardless of how the internal circuit is represented.
See also
Notes
- ^ H. Helmholtz (1853) "Über einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern mit Anwendung auf die thierisch-elektrischen Versuche" [Some laws concerning the distribution of electrical currents in conductors with applications to experiments on animal electricity], Annalen der Physik und Chemie, vol. 89, no. 6, pages 211–233, available online http://gallica.bnf.fr/ark:/12148/bpt6k151746.image.f225.langFR
- ^ L. Thévenin (1883) "Extension de la loi d’Ohm aux circuits électromoteurs complexes" [Extension of Ohm’s law to complex electromotive circuits], Annales Télégraphiques (Troisieme série), vol. 10, pages 222–224. Reprinted as: L. Thévenin (1883) "Sur un nouveau théorème d’électricité dynamique" [On a new theorem of dynamic electricity], Comptes Rendus hebdomadaires des séances de l’Académie des Sciences, vol. 97, pages 159–161.
- ^ Don H. Johnson (April 2003) "Equivalent circuit concept: the voltage-source equivalent," Proceedings of the IEEE, vol. 91, no. 4, pages 636-640. Available on-line at: http://www.ece.rice.edu/~dhj/paper1.pdf .
External links
- Origins of the equivalent circuit concept
- Thevenin's theorem at allaboutcircuits.com
- ECE 209: Review of Circuits as LTI Systems — At end, shows application of Thévenin's theorem that turns complicated circuit into a simple first-order low-pass filter voltage divider with obvious time constant and gain.
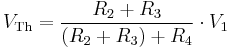
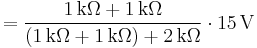
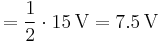
![R_\mathrm{Th} = R_1 %2B \left [ \left ( R_2 %2B R_3 \right ) \| R_4 \right ) ]](/2012-wikipedia_en_all_nopic_01_2012/I/15ffdad3cc8138303ccb784e55d8781a.png)
![= 1\,\mathrm{k}\Omega %2B \left [ \left ( 1\,\mathrm{k}\Omega %2B 1\,\mathrm{k}\Omega \right ) \| 2\,\mathrm{k}\Omega \right ) ]](/2012-wikipedia_en_all_nopic_01_2012/I/5e1391578190a7ec9d47c43918d3a49b.png)